A Merkle Tree allows computers on a network to verify individual records without having to review and compare versions of the entire database. They do so by using cryptography that reveals an individual record while also guaranteeing that all the other records in the database haven’t been changed. First patented in 1979 by Ralph Merkle, Merkle trees have been an important key to database verification throughout the history of computers.
Merkle Trees are especially useful for distributed networks where multiple computers keep copies of the same database or ledger. When Satoshi created Bitcoin, using a Merkle tree for transaction verification was a no-brainer. Because of the distributed nature of the blockchain, we need a secure and fast way to make sure everyone on the network has the same ledger.
If you’ve studied blockchain, then you’ve likely heard about Merkle trees and Merkle roots. However, many investors and enthusiasts don’t know how they work. Considering they are a key part of blockchain security and trust, it’s worth understanding the basics. This ingenious mechanism makes storage and retrieval of millions of blockchain transactions possible.
The Need for Efficient Verification
Let’s start with the basics. Why do we need Merkle trees and what makes them useful in the blockchain context?
To answer that question, consider a world without Merkle trees for verification. If Bitcoin didn’t have Merkle trees, every node on the network would have to keep a complete copy of every single transaction that has ever occurred on Bitcoin. Then, when confirming a past transaction, a node would have to reach out to the network and get copies of the ledger from its peers. Line-by-line, the node would need to compare each entry to its own records to make sure the network ledgers matched exactly. If any alterations slipped through, it would compromise the security of the network.
Because validating the data requires having the data itself, every single verification request on Bitcoin would require enormous packets of information be sent over the network. Then, the validating computer would need to dedicate processing power to comparing the ledgers to make sure there are no changes.
Merkle trees solve this problem by hashing the records in a ledger. This effectively decouples the proof of the data from the data itself. These hashes are orders of magnitude smaller than the ledger itself, so proving a transaction’s validity only involves sending small packets across the network. It allows you to prove that two versions of a ledger are consistent with minimal computing power and network bandwidth.
If that sounds great, it’s because it is. Merkle trees are a really cool cryptographic invention. So, now the question is how do they work?
A Quick Refresher on Hashing
Before we get into the details of Merkle trees, we need cryptographic foundations in hashing. Blockchains use hashing all over the place, from proof of work algorithms to file verification. Hashing is the cornerstone of modern cryptography.
Without getting too far into the weeds, a hash is a type of algorithm that takes any input, no matter the length, and outputs a standard-length, random output. For example, in Bitcoin, the transaction “Alice sends Bob 1 BTC” ends up looking like a string of random characters:
“3cbcf3e1075b0b3357140de438336733bd6927cd1e78d36cc278324fcce932ad”
This string of characters is the hash, and it’s deterministic. That means that “A -> B 1BTC” always hashes to the same output.
However, hashes have another great property. Even a small change in the input avalanches to a drastic change in the output. If we slightly modify the transaction to “A-> B 1.1BTC,” then the hash becomes completely different. Therefore, it’s immediately obvious if a record has been changed even by one character.
Hashes are awesome for other reasons as well, but understanding that hashes are deterministic and changes produce a waterfall is enough to get how a Merkle tree works.
How You Make a Merkle Tree
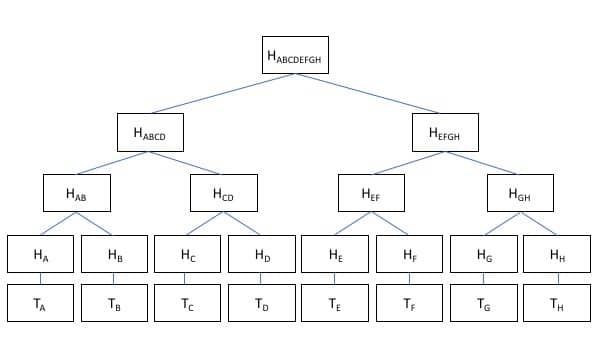
A Merkle tree. Blockchain Merkle trees include thousands of hashes. Only 8 are pictured here.
Now, it’s time to build our Merkle tree. We’ll call our Allice/Bob transaction above “Transaction A.” When that transaction is added to the blockchain, it becomes part of a block with other transactions. For simplicity, we’ll just call those transactions B, C, and D.
Each of those transactions gets hashed, so we don’t have to hold onto the details of who and how much the transaction was. But, we can still prove that the transaction hasn’t been tampered with because we have all the hashes. Now, we have H(A), H(B), H(C), and H(D).
Holding onto four hashes isn’t that big of a deal. However, each Bitcoin block contains around 2,000 transactions, so holding onto and transmitting all those hashes is too much storage and bandwidth. A Merkle tree solves that problem by pairing transactions up and hashing them together.
Now, H(A) + H(B) = H(AB) and H(C)+H(D)=H(CD). By combining and hashing together the transactions, we reduced the number of hashes we have to store by half. We can do the same thing again so H(AB) + H(CD) = H(ABCD). By so doing, we now only have one hash to store that is deterministic based on the hashes of all the underlying transactions. This single hash is called the Merkle root.
Verifying Transactions Using the Merkle Root
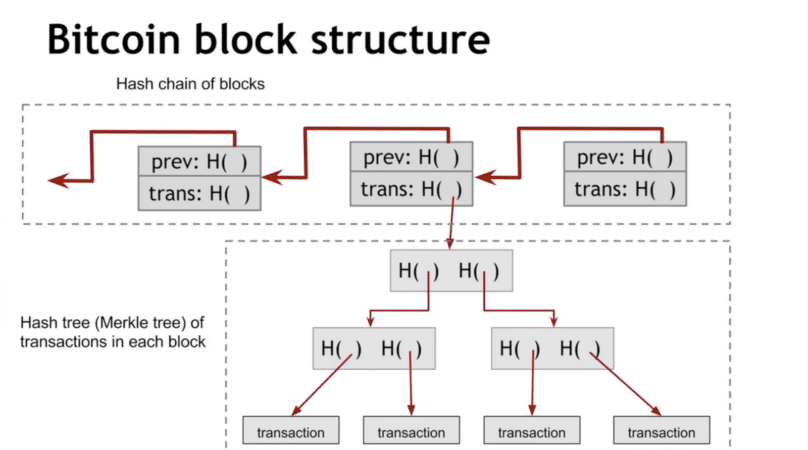
The root hash of the Merkle tree is a key part of each Bitcoin block that gets linked to the next block in the chain.
Each Bitcoin block has the Merkle root contained in the block header. It’s how we verify the contents of the block and consistency of multiple ledgers. If my copy of the blockchain has the same Merkle root for a block as your copy of the blockchain, then we know all the transactions in that block are the same and we agree on the ledger. Even a tiny inconsistency would lead to vastly different Merkle roots because of the properties of a hash.
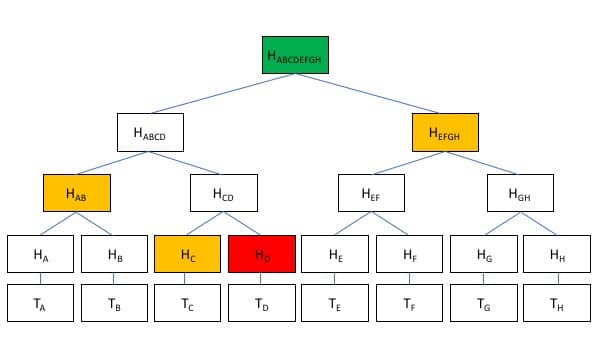
To confirm Transaction D, one only needs to know H(AB), H(C), H(D), and H(EFGH).
If there’s a discrepancy in the Merkle root, I can request the two sub-hashes from a trusted authority. From there, we can narrow down which record we don’t agree on by requesting further sub-hashes. As a result, we can identify discrepancies without having to go line by line through the whole ledger.
Conclusion
Blockchains, databases, and networks around the world use Merkle trees to quickly and efficiently coordinate records across multiple computers. Now that you understand the basics, it’s easy to see why this way of structuring data makes blockchain secure and efficient.
The post Merkle Tree Hashing: How Blockchain Verification Works appeared first on CoinCentral.

Coincentral.com is author of this content, TheBitcoinNews.com is is not responsible for the content of external sites.
Our Social Networks: Facebook Instagram Pinterest Reddit Telegram Twitter Youtube










