Since the recent Bitcoin Cash (BCH) upgrade, the protocol now has some newly added features like the re-enabled opcode OP_Checkdatasig. After the implementation, a few developers have been experimenting with the opcode and have developed concepts such as “spending constraints.” Moreover, in another instance, a programmer recently used the opcode to create an onchain chess game on the BCH blockchain.
Also Read: BCH Upgrades: What’s New and What’s Next
Spending Constraints
Over the last week, BCH supporters have been slowly trying to move away from the recent blockchain split and concentrate on building. One example of this is a recent proof-of-concept written by a BCH developer called Pein Sama, which uses the opcode OP_Checkdatasig to explore new capabilities. Sama details that before the Bitcoin Cash upgrade, the BCH script was limited to someone specifying that one could spend a coin but at the time there was no way of adding constraints on how it could be spent. The developer then demonstrates how it is now possible to create spending constraints with the new BCH coding language called Spedn.
After Sama published his idea, the BCH community discussed the concept of spending constraints and other ideas like covenants as well. A few people specifically discussed the end of Sama’s documentation, which says the concept could produce things like OP_Return based tokens that are “miner enforceable.” The programmer explained that it could be argued that OP_Group is a cleaner way of adding native tokens, but he didn’t have a strong opinion on the matter. “My article is just exploring the new land,” the developer noted on the Reddit forum r/btc.
A Game of Chess
Not long after the published post about spending constraints with the opcode OP_Checkdatasig, a developer named Tobias Ruck was inspired by the opcode exploration and designed a chess game with the new feature. Because chess rules are deterministic, they can use a third party to help enforce the rules of the game and that’s where OP_Checkdatasig comes into play. By utilizing the “nifty spending constraints” originally published by Sama, Ruck shows how the concept can be applied to a game of chess.
“The good thing about chess is that its rules are deterministic, so no need to throw dice or do some cryptographically secure pseudo-random number generator magic,” Ruck explained in his recent blog post. The developer continued by describing the benefits of using OP_Checkdatasig as trusted oracle within a game of chess by stating:
If Kasparov were to challenge Anand for a round of chess, they might trust some third party (referee) or even each other to enforce/follow the rules, but if they are anonymous people on the internet playing for not insignificant amounts of money, it would be good if the rules of the games didn’t require a trusted third party.
In his blog post, Ruck further elaborated how chess can be played with the new opcode and implemented the concept into a Python environment. This is where Ruck adds the “juicy parts” of the code, like operations such as “apply_move,” “white_has_won,” “black_has_won” and “is_stalemate.” After messing around with the program some more, Ruck eventually runs into the situation where a stalemate occurs and the game ends as a draw. Ruck explains that if the game was being played for a 1,000 satoshi incentive “neither white nor black can get any of the 1,000 satoshis, except if they agree to a draw and split the money.”
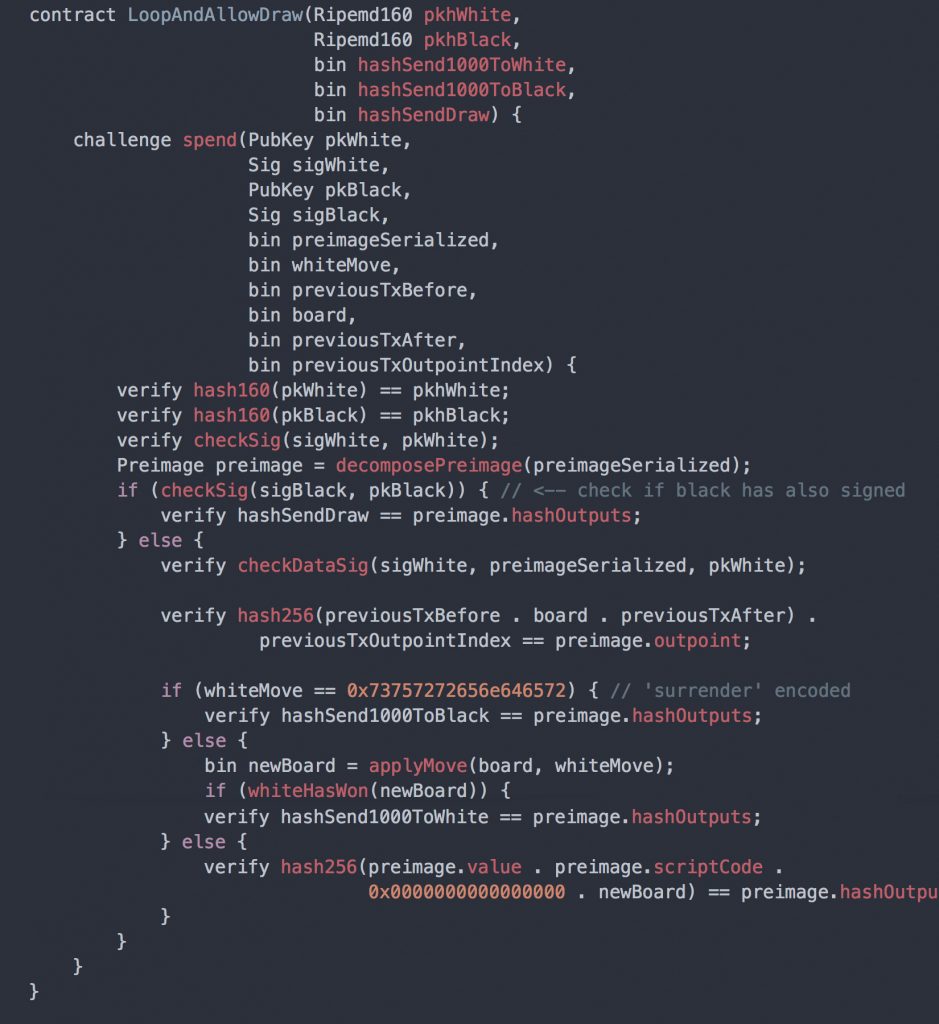
The chess game creator also explains there are a few issues that could arise, like someone not making a move and the 1,000 satoshis getting locked into the blockchain forever. But Ruck says that a lock time could be added and the game will end after a certain amount of time has passed. Overall, Ruck’s chess concept is extremely raw and basic but shows how the opcode could be applied to all types of decision-based games. In conclusion, the developer’s blog post states that he hopes he was able to convey the idea of a chess game using OP_Checkdatasig as trusted and autonomous referee.
Building a Turing Machine on Top of the Bitcoin Protocol
After publishing the onchain chess game and while experimenting with the new opcode, Ruck realized that it is possible to build a Turing machine on top of the Bitcoin protocol. The researcher published a followup post, which shows how he simulated an old programming language using the BCH script.
“A simple way to show Turing completeness is by simulating a Turing machine,” Ruck details in his second blog post. “For that, we’ll pick a derivative of Smallfuck, an esoteric programming language, which has been shown to be Turing complete — If we can simulate that on Bitcoin, we know it’s Turing complete,” the programmer adds.
After showing how it can be done using the new opcode OP_Checkdatasig, Ruck emphasized that the Bitcoin protocol is Turing complete giving the technology a myriad of use cases. Ruck further adds that if developers optimized the code a “fully fledged and operational Bitcoin virtual machine (VM)” could be built. Ruck also adds that people who claim Craig Wright’s propositions “were right about OP_Checkdatasig introducing loops in the Bitcoin script are just wrong” and this is “false” information. “The idea that you could call another transaction by checking a signature is just ludicrous,” Ruck’s blog post states. In order to keep loops spinning, Ruck’s details that the program has to be fed with more satoshis per loop in a similar fashion to the Ethereum network’s gas limit.
What do you think about the chess game that uses the BCH opcode OP_Checkdatasig as an autonomous referee? Let us know what you think about this subject in the comments section below.
Images via Shutterstock, Honest.cash, Pein Sama, Pixabay, and Tobias Ruck.
Express yourself freely at Bitcoin.com’s user forums. We don’t censor on political grounds. Check forum.Bitcoin.com.
The post New Bitcoin Cash Opcode Shows an Onchain Game of Chess is Possible appeared first on Bitcoin News.
Bitcoin.com is author of this content, TheBitcoinNews.com is is not responsible for the content of external sites.
Our Social Networks: Facebook Instagram Pinterest Reddit Telegram Twitter Youtube
